本文共 4786 字,大约阅读时间需要 15 分钟。
说在前面
这篇博客主要介绍怎么解决多分类问题?下面我们解决多分类问题的时候会用到 Softmax Classifier,下面我们就来看看 Softmax 分类器怎么解决多分类问题的以及我们如何实现。
上一篇博客我们对糖尿病数据集进行了二分类,我们最后输出的是
y = 1 y=1 y=1 的概率和
y = 0 y=0 y=0 的概率。因为我们只有两个分类,所以我们只需要算出一个分类的概率,另一个分类的概率直接用 1 减去上一个分类的概率即可。
但实际上,我们还介绍了一些其他数据集,比如 MNIST(手写数字),这个数据集的分类一共有 10 类(分别是数字 0-9),下面我们主要讨论两个话题:第一个是怎么用 Softmax 分类器来解决 MNIST 数据集多分类问题?第二个就是我们怎么使用 Pytorch 去实现?
多分类问题
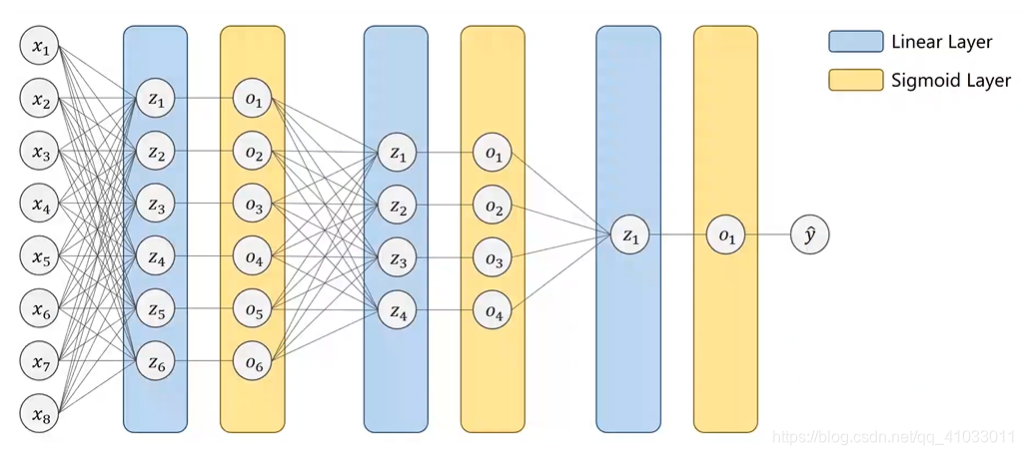
如果你有 10 个分类,那么你怎样设计神经网络?第一种设计的方式就是由原来的一个输出变成 10 个输出,即输出分别等于 0–9 的概率值。

这样我们就能输出它属于每个分类的概率,但是需要注意的是,我们这里是把每一个类别看做是一个二分类问题。那么这里会存在一些问题,因为一个样本肯定是属于 10 个类别中的一个,所以最后的 10 个输出应该是互相抑制的。再举个简单例子,假设上图中
O 1 O_1 O1 值输出为 0.8,那它就得抑制后面的其它输出要变小。但是我们用这种方法解决多分类问题,我们是没办法解决抑制问题的,所以我们最好不要输出它属于每个类别的概率,比如说,一个样本属于
y 1 y_1 y1 的概率为 0.8,属于
y 2 y_2 y2 的概率为 0.8,属于
y 3 y_3 y3 的概率为 0.9,单从概率值上来看,
y 3 y_3 y3 应该比另外两个更有可能,但是
y 1 y_1 y1 说它有 80% 的可能属于
y 1 y_1 y1,
y 3 y_3 y3 有 90% 的可能属于
y 3 y_3 y3,其实这二者是互相矛盾的。所以我们希望我们将来输出的10个输出能够
满足分布上的要求,即
每个输出都要大于 0,还有就是 10 个输出的和等于 1。
所以在处理多分类问题的时候,我们在神经网络前面的一些层里还是使用 Sigmoid 函数,但是我们最终输出层不再使用 Sigmoid,因为 Sigmoid 得不到我们想要的结果,我们需要做的是一个 Softmax 层,它能够输出一个分布,它满足分布需要的两个条件。

那下面我们就来看看 Softmax 是怎么实现的?它怎么保证将最后的输出都大于 0,还有就是让所有的输出值的和为 1。
假设用
Z l Z^l Zl 表示第
l l l 层的输出,它是最后一个线形层的输出,那么 Softmax 函数表达式如下:
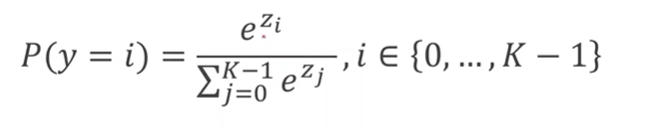
对于 Z l Z^l Zl 来说,它有多个输出,比如 z 0 z_0 z0 到 z k − 1 z_k-1 zk−1(假设有 k k k 个分类),我们得先算分子 z i z_i zi 的指数,这里为什么要用到 e^( z i z_i zi) 呢?因为指数的运算得到的结果永远是大于 0 的。然后分母的计算就是将 e^( z 0 z_0 z0) 一直加到 e^(z_k-1),就是将每个分类的输出进行求和。让每一项都除以它们的和目的就是为了满足每个分类结果相加之和为 1。
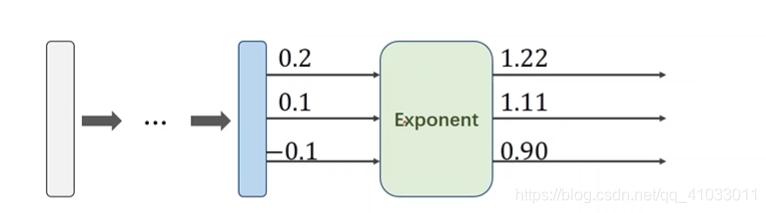
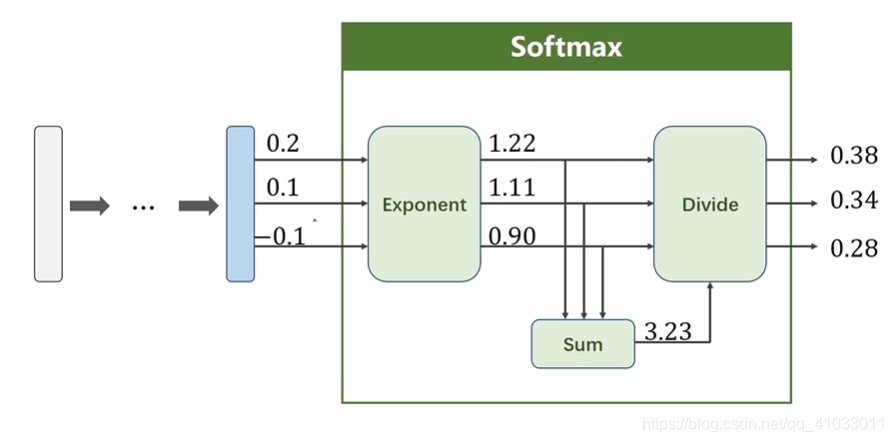
下面举个简单的例子。比如现在有 3 个分类,那么经过线性层的空间变换后我们有三个输出值:

第一步我们对每一个输出结果进行指数运算将其转换成大于 0 的值:
为了使得它们的和为 1,所以三个值分别除以它们的和:
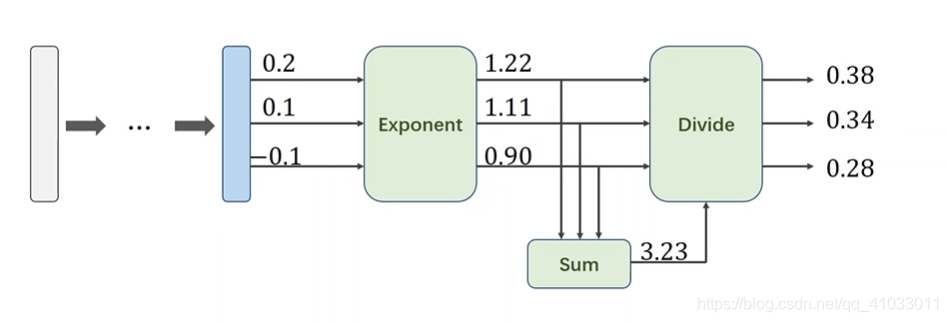
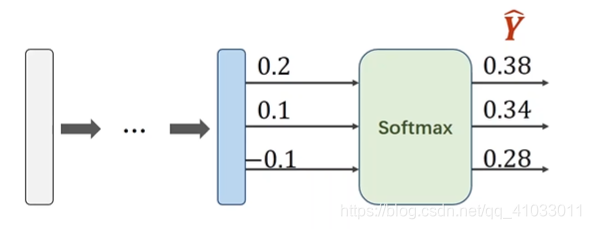
那么最后就形成了一个分布。有了分布之后,我们才能够更好的设计损失函数。我们把输入的值经过指数运算,然后分别除以它们的和,我们把这一过程称做 Softmax。
那么我们用 Softmax 得到分布后,我们怎么定义损失函数?
之前的二分类问题用的是交叉熵的方式作为损失函数:
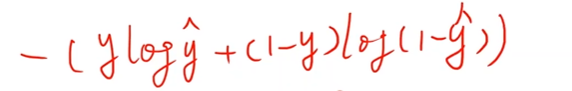
所以实际上对于两个分类来说,将来求和的时候有两项,但是这两项在任何时候只有一个值是非零的,如果
y = 0 y=0 y=0,即样本标签是 0,那么
y l o g y ylogy ylogy 该项就是 0;同理,如果
y = 1 y=1 y=1,即样本标签是 1,那么
( 1 − y ) l o g ( 1 − y ) (1-y)log(1-y) (1−y)log(1−y) 该项就是 0。所以我们扩展到多分类之后,我们要使得:

所以我们的 Loss 函数变成了:
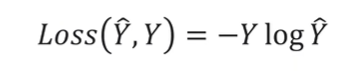
那么我们就可以将 Loss 过程分解成先进行 Log 运算,再与
Y Y Y 相乘:
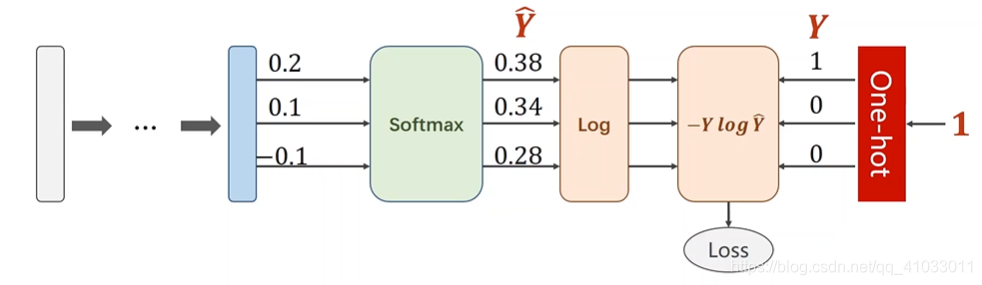
以我们将下面框中的过程称做 NLLLoss。

下面是我们用代码实现 NLLLoss 过程:
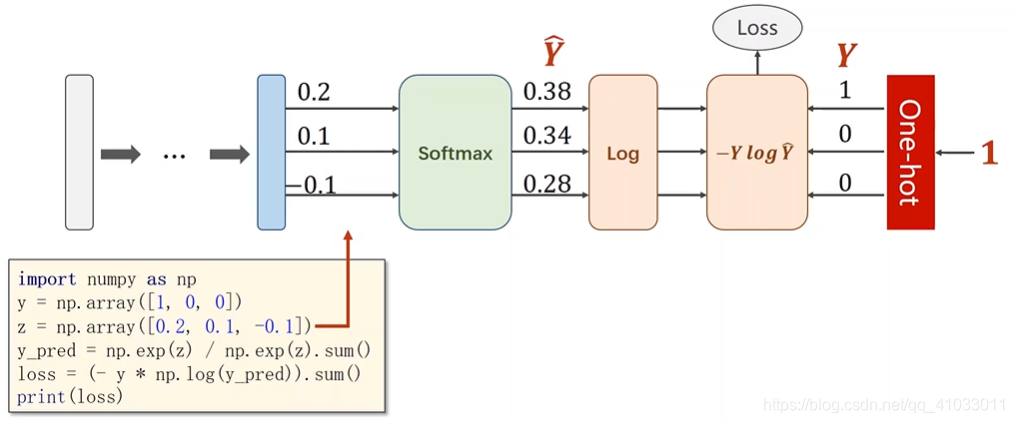

将在 Pytorch 里面提供了一个更常用的损失:
交叉熵损失。这个损失从 Softmax 开始,然后求对数,到得到结果为止的整个过程叫做交叉熵损失。
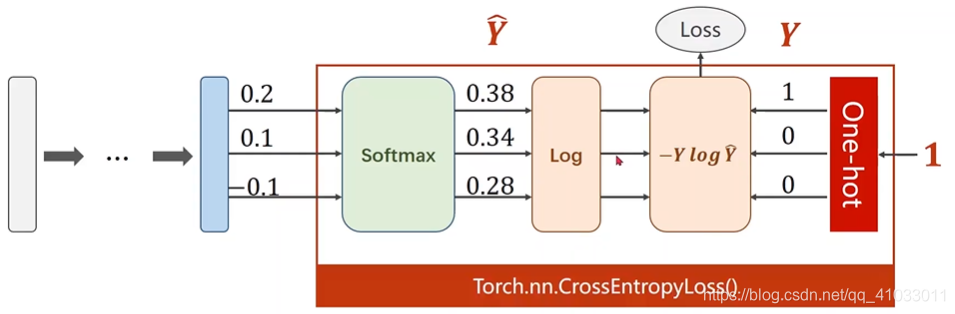
所以在我们使用交叉熵损失的时候,我们
神经网络的最后一层是不做激活的,因为把它们变成分布的激活函数是包括在交叉熵损失里面的,所以最后一层不要做非线性变换,直接将结果交给交叉熵损失即可。在做交叉熵损失时,需要注意
y y y 是一个 LongTensor,是一个
长整型的张量。

下面我们看一个具体例子:现在我们有 3 个样本,这 3 个样本分别是属于第 2 类,第 0 类,第 1 类。

假设我们现在有两组预测:Y_pred1 和 Y_pred2,我们看一下它们的损失结果是怎样的?我们通过计算可以分别得出两组预测值的交叉熵损失:

很显然,第二个预测的交叉熵更大一些,而且我们从数据也能看出来,第一个预测是比较好的,所以它的交叉熵相应的也更小一些。
有了 Softmax 和 交叉熵损失之后,我们再回过头看怎么处理 MNIST 数据集的多分类问题。
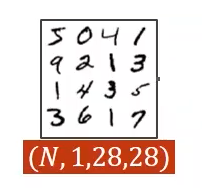
下面是一个手写数字数据集中的一个图像:

该图像中,颜色越深表示其中的数值越小,最小为 0;越亮的地方表示数值越大,最大为 255。MNIST 数据集中每一张图像都是 28*28=784 个像素点,每个像素点的取值是 0-255,如果我们将它们的数值映射到 0-1 之间,表示如下:

那么我们要实现这样一个多分类的问题,那么我们写代码的步骤还是那四步:唯一的区别就是第四步时加上了测试数据集。

代码实现
接下来我们看一下代码实现:
1. Prepare Dataset
一开始,我们需要引入相关的包,其中与数据集相关的包有 transforms,Dataset 和 DataLoader。transforms 主要是对原始图像或者数据进行一些各种各样的处理。

其中我们改用 ReLU 函数作为激活函数,不使用 Sigmoid 函数。
然后还有就是优化器。
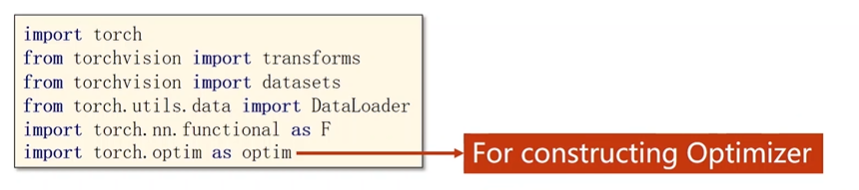
接下来先来看一下我们这个处理,我们这个处理里面数据的准备和以前的区别在哪呢?首先我们定义 batch-size 的大小。然后我们定义了一个 transform。我们在读取图像的时候使用的是 Python 的 PIL,然后得到的图像再用神经网络进行处理的时候,它希望处理的数值比较小,最好是在 +1 到 -1 之间,就是输入最好能够遵从正态分布,这样的输入对于神经网络的训练是最有帮助的。

那么首先要把原始图像转变成一个图像张量,然后它的像素值是 0-1。

下面补充一下图像里面的知识,在视觉里面的图像,比如一个黑白灰度图看上去就像是一个矩阵,但实际上它并不是一个矩阵,我们把它叫做单通道的图像,那么相应的,就有多通道,比如看到的彩色图像,有 R、G、B 三个通道。
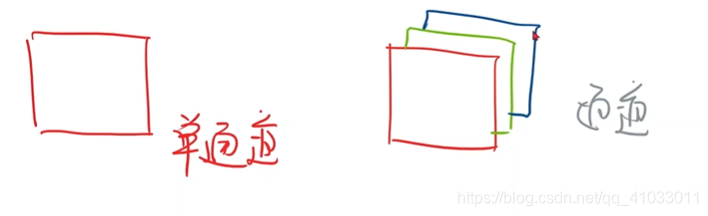
在通道里面,图像有高度(H)和 宽度(W)。
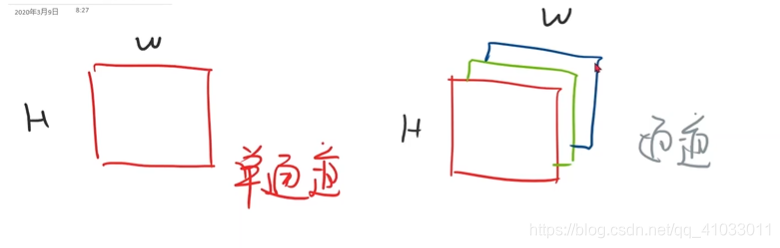
那么对于多通道图像来说,通道这个单词是 Channel,我们通常用
C C C 表示通道。然后我们在表示图像的时候,就是说我们用 PIL 或者 OpenCV 读进来的图像张量一般都是
W W W x
H H H x
C C C 这样的顺序。然后在 Pytorch 中,我们要把它的顺序转换成
C C C x
W W W x
H H H,就是要把通道放在前面,这是为了在 Pytorch 中进行更高效的图像处理和卷积运算而做的转换。
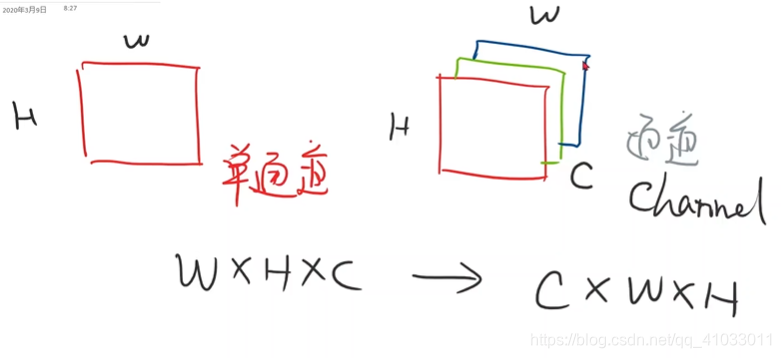
所以我们在拿到图像之后,我们就需要先把图像转换成 Pytorch 里面的 Tensor。

之后要做的事情就是将 0-255 的值映射到 0-1 之间,然后把它的维度从 28x28 变成 1x28x28 这样的张量,即由单通道变为多通道。那么这个过程我们就可以用 transforms 提供的 ToTensor 这样一个对象来实现。
我们注意到 transforms 构造的是 Compose 这样一个类的实例:

Compose 相当于 Pipeline(管道),可以把 [] 括起来一系列的对象按照顺序来处理。之后接下来做的是 Normalize(归一化)。下面给出的均值和标准差是一个经验值,以后的过程中直接使用就可以了。


那么以后我们拿到一个图像,先将它转换成张量,然后再进行数据归一化,最后供神经网络进行训练。前面反复提到过 0-1 分布的数据训练神经网络的效果是最好的。
我们的 transform 定义好之后,我们直接将它放到数据集之中。
2. Design Model
之后再来看一下我们怎么 Design Model。我们的输入是一组图像,我们的激活层变成了 ReLU,最后的输出层是不做激活的。
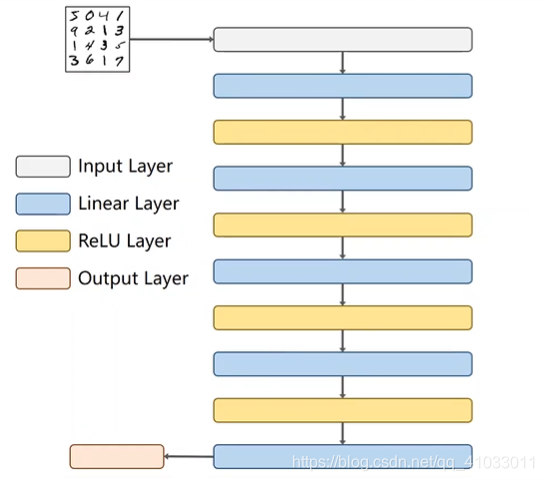
因为我们使用的是 mini-batch,所以我们的输入是一个四阶的张量,每个张量里面有
N N N 个样本,每个样本是 1 维的 28x28 的图像。
但是在全连接神经网络中,我们要求输入是一个矩阵。所以接下来的第一步就是把 1x28x28 三阶的张量转换成 1 阶的向量,所以最后形成了有 784 个元素的向量。我们可以用下列代码进行转换:

然后经过第一个线性层处理之后,比如说从 784 降到了 512,那么相应的代码就是:

然后接着做一个非线性的变换,即是用 ReLU 函数:

然后我们把 512 降到了 256,然后再做一个激活。

以此类推,直到最后一层我们将它降到了 10,就不再进行激活了。最后我们再通过 Softmax 将其变为概率。那么我们整个网络的流程图大致如下:

有了这个流程图之后,我们就可以很快写出相应的代码。

然后我们选用的损失函数和优化器有相应的一些变化。

第一个就是交叉熵损失经过 Softmax,Log ,然后再做一个向量乘法得到 Loss。另外在优化器中仍然使用 SGD,但是由于我们的模型相对比较复杂了,所以使用更好一些的优化算法,比如说把冲量值(momentum)设置为 0.5,来优化它的训练过程。
最后再来看一下训练过程,因为在训练过程中还涉及到了测试,为了代码的可读性,所以我们将一轮循环封装成函数 train。

在 test 中只需要计算前向传播,然后得出最后的分类是多少即可,不需要做反向传播。

那么我们的训练过程代码如下:

那么整个程序到这也就结束了,具体代码见
转载地址:http://pooi.baihongyu.com/



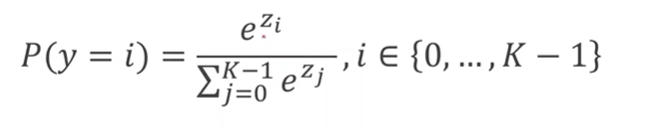

 为了使得它们的和为 1,所以三个值分别除以它们的和:
为了使得它们的和为 1,所以三个值分别除以它们的和:  那么最后就形成了一个分布。有了分布之后,我们才能够更好的设计损失函数。我们把输入的值经过指数运算,然后分别除以它们的和,我们把这一过程称做 Softmax。
那么最后就形成了一个分布。有了分布之后,我们才能够更好的设计损失函数。我们把输入的值经过指数运算,然后分别除以它们的和,我们把这一过程称做 Softmax。 

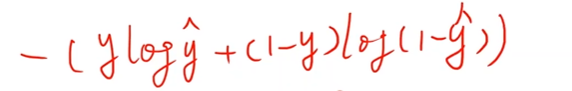
 所以我们的 Loss 函数变成了:
所以我们的 Loss 函数变成了: 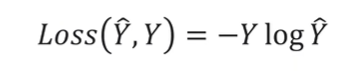
 以我们将下面框中的过程称做 NLLLoss。
以我们将下面框中的过程称做 NLLLoss。 

















 之后要做的事情就是将 0-255 的值映射到 0-1 之间,然后把它的维度从 28x28 变成 1x28x28 这样的张量,即由单通道变为多通道。那么这个过程我们就可以用 transforms 提供的 ToTensor 这样一个对象来实现。 我们注意到 transforms 构造的是 Compose 这样一个类的实例:
之后要做的事情就是将 0-255 的值映射到 0-1 之间,然后把它的维度从 28x28 变成 1x28x28 这样的张量,即由单通道变为多通道。那么这个过程我们就可以用 transforms 提供的 ToTensor 这样一个对象来实现。 我们注意到 transforms 构造的是 Compose 这样一个类的实例: 


 因为我们使用的是 mini-batch,所以我们的输入是一个四阶的张量,每个张量里面有 N N N 个样本,每个样本是 1 维的 28x28 的图像。
因为我们使用的是 mini-batch,所以我们的输入是一个四阶的张量,每个张量里面有 N N N 个样本,每个样本是 1 维的 28x28 的图像。 

 然后接着做一个非线性的变换,即是用 ReLU 函数:
然后接着做一个非线性的变换,即是用 ReLU 函数: 




 在 test 中只需要计算前向传播,然后得出最后的分类是多少即可,不需要做反向传播。
在 test 中只需要计算前向传播,然后得出最后的分类是多少即可,不需要做反向传播。  那么我们的训练过程代码如下:
那么我们的训练过程代码如下: 